The powerful Keras framework (which supplements other machine learning technologies such as Tensorflow) provides a set of inbuilt activation functions which provide a alternative behaviours for different machine learning scenarios.
elu - Exponential Linear Unit
keras.activations.elu(x, alpha=1.0)
Arguments
- x: Input tensor
- alpha: A scalar, slope of negative section
Returns
The exponential linear activation: x if x > 0 and alpha * (exp(x) -1) if x < 0
softmax
keras.activations.softmax(x, axis=-1)
Arguments
x: Input tensor. axis: Integer, axis along which the softmax normalization is applied.
Returns
Tensor, output of softmax transformation.
\[\sigma(z)_i = \frac{e^z}{\sum_{j=1}^{K} e^{zj}} \textrm{for i}=1,...,K \textrm{ and z} = (z_1, ... , z_K) \epsilon \R ^ K\]Comment (Source)
In mathematics, the softmax function, also known as softargmax or normalized exponential function, is a function that takes as input a vector of K real numbers, and normalizes it into a probability distribution consisting of K probabilities proportional to the exponentials of the input numbers. That is, prior to applying softmax, some vector components could be negative, or greater than one; and might not sum to 1; but after applying softmax, each component will be in the interval (0,1), and the components will add up to 1, so that they can be interpreted as probabilities. Furthermore, the larger input components will correspond to larger probabilities. Softmax is often used in neural networks, to map the non-normalized output of a network to a probability distribution over predicted output classes.
If we take an input of [1, 2, 3, 4, 1, 2, 3], the softmax of that is [0.024, 0.064, 0.175, 0.475, 0.024, 0.064, 0.175]. The output has most of its weight where the ‘4’ was in the original input. This is what the function is normally used for: to highlight the largest values and suppress values which are significantly below the maximum value. But note: softmax is not scale invariant, so if the input were [0.1, 0.2, 0.3, 0.4, 0.1, 0.2, 0.3] (which sums to 1.6) the softmax would be [0.125, 0.138, 0.153, 0.169, 0.125, 0.138, 0.153]. This shows that for values between 0 and 1 softmax, in fact, de-emphasizes the maximum value (note that 0.169 is not only less than 0.475, it is also less than the initial proportion of 0.4/1.6=0.25)
>>> import numpy as np
>>> a = [1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0]
>>> np.exp(a) / np.sum(np.exp(a))
array([0.02364054, 0.06426166, 0.1746813, 0.474833, 0.02364054,
0.06426166, 0.1746813])
selu - Scaled Exponential Linear Unit
keras.activations.selu(x)
Arguments
x: A tensor or variable to compute the activation function for
Returns
The scaled exponential unit activation: scale * elu(x, alpha)
Comment Source
SELU is equal to: scale * elu(x, alpha), where alpha and scale are predefined constants. The values of alpha and scale are chosen so that the mean and variance of the inputs are preserved between two consecutive layers as long as the weights are initialized correctly (see lecun_normal initialization) and the number of inputs is “large enough” (see references for more information).
softplus
keras.activations.softplus(x)
Arguments
x: Input tensor
Returns
The softplus activation: $log(exp(e) + 1)$
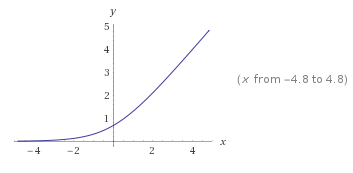
Softsign
keras.activations.softsign(x)
Arguments
x: Input tensor.
Returns
The softsign activation: $\frac{x}{\lvert{x}\rvert + 1}$
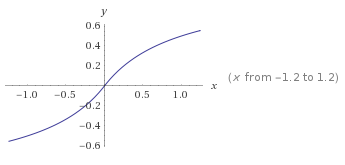
ReLu
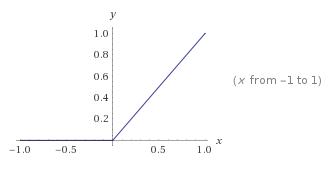
Rectified Linear Unit
This popular activation function is used
- typically found used in
- convolutional neural networks
- multi-layer networks
- pass positive sum evaluations (unaltered)
- small positive values only contribute a small amount to the next layer
- removes negative sum evaluations from contributing to the next layer
- small or large negative values are treated equally
- effectively diminishes the impact of ancestors of the activating neuron on the next layer
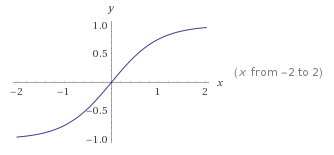
tanh - Hyperbolic tangent
keras.activations.tanh(x)
Arguments
x: Input tensor.
Returns
The hyperbolic activation: $tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$.
Sigmoid
keras.activations.sigmoid(x)
Arguments
x: Input tensor.
Returns
The sigmoid activation: $\frac{1}{1 + e^{-x}}$.
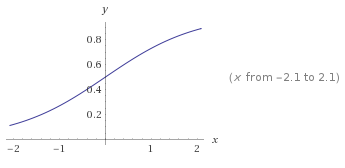
Hard Sigmoid
keras.activations.hard_sigmoid(x)
Faster to compute than sigmoid activation.
Arguments
x: Input tensor.
Returns
Hard sigmoid activation:
\[y = \begin{cases} 0 &\text{ if x < -2.5 } \\ 1 &\text{ if x > 2.5 } \\ 0.2 * x + 0.5 &\text{ if -2.5 <= x <= 2.5 } \end{cases}\]